人教版小升初数学知识点汇总_人教版小升初数学知识要点整理

【#小升初# 导语】天高鸟飞，海阔鱼跃，学习这舞台，秀出你独特的精彩用好分秒时间，积累点滴知识，解决疑难问题，学会举一反三。以下是®文档大全网为大家整理的《人教版小升初数学知识要点整理》供您查阅。

　　（一）数的认识

　　整数【正数、0、负数】

　　一、一个物体也没有，用0表示。0和1、2、3……都是自然数。自然数是整数。

　　二、最小的一位数是1，最小的自然数是0。

　　三、零上4摄氏度记作+4℃；零下4摄氏度记作-4℃。“+4”读作正四。“-4”读作负四。 +4也可以写成4。

　　四、像 +4、19、+8844这样的数都是正数。像-4、-11、-7、-155这样的数都是负数。

　　五、0既不是正数，也不是负数。正数都大于0，负数都小于0。

　　六、通常情况下，比海平面高用正数表示，比海平面低用负数表示。

　　七、通常情况下，盈利用正数表示，亏损用负数表示。

　　八、通常情况下，上车人数用正数表示，下车人数用负数表示。

　　九、通常情况下，收入用正数表示，支出用负数表示。

　　十、通常情况下，上升用正数表示，下降用负数表示。

　　

　　小数【有限小数、无限小数】

　　一、分母是10、100、1000……的分数都可以用小数表示。一位小数表示十分之几，两位小数表示百分之几，三位小数表示千分之几……

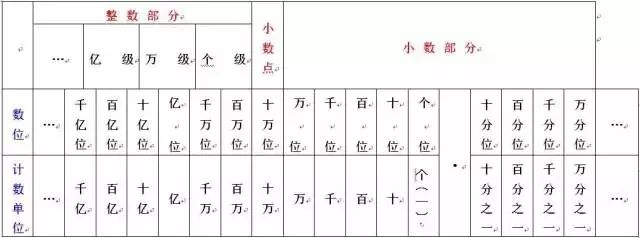
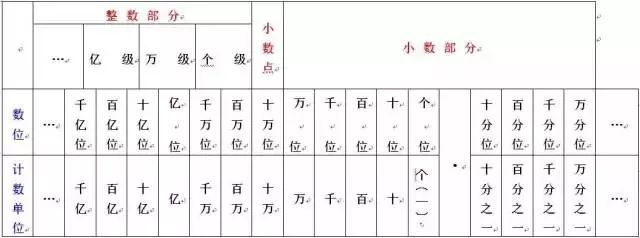
　　二、整数和小数都是按照十进制计数法写出的数，个、十、百……以及十分之一、百分之一……都是计数单位。每相邻两个计数单位间的进率都是10。

　　三、每个计数单位所占的位置，叫做数位。数位是按照一定的顺序排列的。

　　四、小数的性质：小数的末尾添上“0”或去掉“0”，小数的大小不变。

　　五、根据小数的性质，通常可以去掉小数末尾的“0”，把小数化简。

　　六、比较小数大小的一般方法：先比较整数部分的数，再依次比较小数部分十分位上的数，百分位上的数，千分位上的数，从左往右，如果哪个数位上的数大，这个小数就大。

　　七、把一个数改写成用“万”或“亿”作单位的数，在万位或亿位右边点上小数点，再在数的后面添写“万”字或“亿”字。

　　八、求小数近似数的一般方法：1先要弄清保留几位小数；2根据需要确定看哪一位上的数；3用“四舍五入”的方法求得结果。

　　九、整数和小数的数位顺序表：

　　

　　分数【真分数、假分数】

　　一、把单位“1”平均分成若干份，表示这样的一份或几份的数叫做分数。表示其中一份的数，是这个分数的分数单位。

　　二、两个数相除，它们的商可以用分数表示。即：a÷b=b/a（b≠0）

　　三、小数和分数的意义可以看出，小数实际上就是分母是10、100、1000…的分数。

　　四、分数可以分为真分数和假分数。

　　五、分子小于分母的分数叫做真分数。真分数小于1。

　　六、分子大于或等于分母的分数叫做假分数。假分数大于或等于1。

　　七、分子和分母只有公因数1的分数叫做最简分数。

　　八、分数的基本性质：分数的分子和分母同时乘或除以相同的数（零除外），分数的大小不变。

　　九、小数的性质和分数的基本性质一致的，应用分数的基本性质，可以通分和约分。

　　百分数【税率、利息、折扣、成数】

　　一、表示一个数是另一个数的百分之几的数叫做百分数。百分数也叫百分率或百分比，百分数通常用“%”表示。

　　二、分数与百分数比较：

	不同点	相同点
分 数	可以表示具体数量，可以有单位名称	表示两个数之间的关系
百分数	不可以表示具体数量，不可以有单位名称

　　三、分数、小数、百分数的互化。

　　（1）把分数化成小数，用分数的分子除以分母。

　　（2）把小数化成分数，先改写成分母是10、100、1000……的分数，再约分。

　　（3）把小数化成百分数，先把小数点向右移动两位，然后添上百分号。

　　（4）把百分数化成小数，先去掉百分号，然后把小数点向左移动两位。

　　（5）把分数化成百分数，先把分数化成小数（除不尽时通常保留三位小数），再把小数化成百分数。

　　（6）把百分数化成分数，先把百分数改写成分数，能约分的要约成最简分数。

　　四、熟记常用三数的互化。

　　五、

　　1、出勤率表示出勤人数占总人数的百分之几。

　　2、合格率表示合格件数占总件数的百分之几。

　　3、成活率表示成活棵数占总棵数的百分之几。

　　六、求一个数比另一个数多百分之几，就是求一个数比另一个数多的占另一个数的百分之几。

　　七、1、多的÷“1”=多百分之几 2、少的÷“1”= 少百分之几

　　八、应得利息是税前利息，实得利息是税后利息。

　　九、利息 = 本金 × 利率 × 时间

　　十、应得利息 －利息税 = 实得利息

　　十一、几折表示十分之几，表示百分之几十；几几折表示十分之几点几，表示百分之几十几。

　　十二、

　　1、原价×折扣=现价

　　2、现价÷原价=折扣

　　3、现价÷折扣=原价

　　十三、几成表示十分之几表示百分之几十；几成几表示十分之几点几，表示百分之几十几。

　　因数与倍数【素数、合数、奇数、偶数】

　　一、4 × 3 = 12，12是4的倍数，12也是3的倍数，4和3都是12的因数。

　　二、一个数最小的倍数是它本身，没有的倍数。一个数倍数的个数是无限的。

　　三、一个数最小的因数是1，的因数是它本身。一个数因数的个数是有限的。

　　四、5的倍数：个位上的数是5或0。

　　2的倍数：个位上的数是2、4、6、8或0。2的倍数都是双数。

　　3的倍数：各位上数的和一定是3的倍数。

　　五、是2的倍数的数叫做偶数。不是2的倍数的数叫做奇数。

　　六、一个数，如果只有1和它本身两个因数，这样的数就叫做素数（或质数）。

　　七、一个数，如果除了1和它本身还有别的因数，这样的数就叫做合数。

　　八、在1—20这些数中： （1既不是素数，也不是合数）

　　奇数：1、3、5、7、9、11、13、15、17、19。

　　偶数：2、4、6、8、10、12、14、16、18、20。

　　素数：2、3、5、7、11、13、17、19。（共8个，和为77。）

　　合数：4、6、8、9、10、12、14、15、16、18、20。（共11个，和为132。）

　　九、最小的奇数是1，最小的偶数是0，最小的素数是2，最小的合数是4。

　　十、如果两个数是倍数关系，则大数是最小公倍数，小数是公因数。

　　十一、如果两个数只有公因数1，则公因数是1，最小公倍数是它们的乘积。

　　（二）数的运算

　　计算法则【整数、小数、分数】

　　一、计算整数加、减法要把相同数位对齐，从低位算起。

　　二、计算小数加、减法要把小数点对齐，从低位算起。

　　三、小数乘法：1、先按整数乘法算出积是多少，看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

　　2、注意：在积里点小数点时，位数不够的，要在前面用0补足。

　　四、小数除法：

　　1、商的小数点要和被除数的小数点对齐；

　　2、有余数时，要在后面添0，继续往下除；

　　3、个位不够商1时，要在商的整数部分写0，点上小数点，再继续除。

　　4、把除数转化成整数时，除数的小数点向右移动几位，被除数的小数点也要向右移动几位。

　　5、当被除数的小数位数少于除数的小数位数时，要在被除数的末尾用0补足。

　　五、一个小数乘10、100、1000……只要把这个小数的小数点向右移动一位、两位、三位……

　　六、一个小数除以10、100、1000……只要把这个小数的小数点向左移动一位、两位、三位……

　　七、分数加、减法：1同分母分数相加减，把分子相加减，分母不变。2异分母分数相加减，要先通分化成同分母分数，然后再相加减。

　　八、分数大小的比较：1同分母分数相比较，分子大的大，分子小的小。2异分母的分数相比较，先通分然后再比较；若分子相同，分母大的反而小。

　　九、分数乘分数，用分子相乘的积作分子，分母相乘的积作分母。

　　十、甲数除以乙数（0除外），等于甲数乘乙数的倒数。

　　四则运算关系

加法	一个加数 = 和－另一个加数
减法	被减数 = 差 + 减数 　　减数 = 被减数 － 差
乘法	一个因数 = 积 ÷ 另一个因数
除法	被除数 = 商 × 除数 　　除数 = 被除数 ÷ 商

　　两个规律

　　一、除法的商不变规律：被除数和除数同时乘或除以相同的数（0除外），商不变。

　　二、乘法的积不变规律：如果一个因数乘几，另一个因数则除以几，那么它们的积不变。

　　简便计算

　　一、运算定律：

运算定律	用字母表示
加法交换律	a＋b=b＋a
加法结合律	（a＋b）＋c=a＋(b＋c)
乘法交换律	a×b=b×a
乘法结合律	（a×b）×c=a×(b×c)
乘法分配律	（a＋b）×c=a×c＋b×c
减法运算规律	a－b－c=a－（b＋c）
除法运算规律	a÷b÷c=a÷（b×c）

　　二、乘、除法的互化。（小技巧：符号是相反的；两个数相乘得“1”。）

（1）A÷0.1=A×10 　　（2）A×0.1=A÷10	（7）A÷0.01=A×100； 　　（8）A×0.01=A÷100
（3）A÷0.2=A×5 　　（4）A×0.2=A÷5	（9）A÷0.25=A×4 　　（10）A×0.25=A÷4
（5）A÷0.5=A×2 　　（6）A×0.5=A÷2	（11）A÷0.125=A×8 　　（12）A×0.125=A÷8

　　三、求近似数的方法。

　　①四舍五入法。 ②进一法。 ③去尾法。

　　四、积与因数、商与被除数的大小比较：

第2个因数>1,积>第1个因数； 　　第2个因数=1,积=第1个因数； 　　第2个因数<1,积<第1个因数。

除数>1，商<被除数； 　　除数=1，商=被除数； 　　除数<1，商>被除数；

　　数量关系

单价×数量=总价 　　总价÷数量=单价 　　总价÷单价=数量	工作效率×工作时间=工作总量 　　工作总量÷工作时间=工作效率 　　工作总量÷工作效率=工作时间
速度×时间=路程 　　路程÷时间=速度 　　路程÷速度=时间	速度和×相遇时间=路程 　　路程÷相遇时间=速度和 　　路程÷速度和=相遇时间

　　三、式与方程

　　用字母表示数

　　一、在一个含有字母的式子里，数字和字母、字母和字母相乘时，中间的乘号可以记作“· ”，也可以省略不写。在省略数字与字母之间的乘号时，要把数字写在字母的前面。

　　二、2a与a2意义不同：2a表示两个a相加，a2表示两个a相乘。即：2a=a＋a，a2= a×a。

　　三、用字母表示数：

　　①用字母表示任意数：如X=4 a=6

　　②用字母表示常见的数量关系：如s=vt

　　③用字母表示运算定律：如a＋b=b＋a

　　④用字母表示计算公式：S=ah

　　方程与等式

　　一、含有未知数的等式叫做方程。

　　二、使方程左右两边相等的未知数的值，叫做方程的解。

　　三、求方程的解的过程，叫做解方程。

　　四、方程和等式的联系与区别：

	方 程	等 式
联 系	方程一定是等式，等式不一定是方程
区 别	含有未知数	不一定含有未知数

　　五、等式的基本性质（一）：等式两边同时加上（或减去）一个相同的数，所得结果仍然是等式。

　　六、等式的基本性质（二）： 等式两边同时乘（或除以）一个不等于零的数，所得结果仍然是等式。

　　七、列方程解应用题的一般步骤：

　　①弄清题意，找出未知数并用X表示。

　　②找出应用题中数量间的相等关系，并列出方程。

　　③求出方程的解。

　　④检验或验算，写出答案。

　　（四）正比例与反比例

　　比和比例

　　一、比和比例的联系与区别：

比 　　与 　　比 　　例 　　的 　　区 　　别	1、意义不同	比的意义	两个数相除又叫做两个数的比。
比例的意义	表示两个比相等的式子叫做比例。
2、名称不同	比的名称	两点读作比，比号前面的数叫做比的前项，比号后面的数叫做比的后项。
比例的名称	组成比例的四个数叫做比例的项，两端的两项叫做比例的的外项，中间的两项叫做比例的内项。
3、性质不同	比的性质	比的前项和后项同时乘或者除以相同的数（0除外），比值不变。
比例的性质	在比例里，两个外项的积等于两个内项的积。
4、应用不同	应用比的意义	求比值。
应用比的性质	化简比。
应用比例的意义	判断两个不能否组成比例。
应用比例的性质	不但可以判断两个比能否组成比例，还可以解比例。

　　二、比同分数、除法的联系与区别：

	比	分数	除法
联 　　系	前项	分子	被除数
比号	分数线	除号
后项	分母	除数
比值	分数值	商
比的基本性质	分数的基本性质	除法的商不变性质
区 　　别	比表示两个数之间的关系。	分数表示一个数。	除法表示一种运算。

　　三、求比值与化简比的区别：

	一 般 方 法	结 果
求比值	根据比值的意义，用前项除以后项。	是一个数。可以是整数、小数或分数。
化简比	根据比的基本性质，把比的前项和后项都乘或除以相同的数（零除外）。	是一个比。它的前项和后项都是整数，并且是互质数。

　　四、化简比：

　　①整数比的化简方法是：用比的前项和后项同时除以它们的公约数。

　　②小数比的化简方法是：先把小数比化成整数比，再按整数比化简方法化简。

　　③分数比的化简方法是：用比的前项和后项同时乘以分母的最小公倍数。

　　五、比例尺：我们把图上距离和实际距离的比叫做这幅图的比例尺。

　　六、比例尺=图上距离︰实际距离 比例尺 = 图上距离 / 实际距离

　　正比例、反比例

　　一、正比例：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系就叫做正比例关系。

　　二、反比例：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系就叫做反比例关系。

　　三、正比例与反比例的区别：

	正 比 例	反 比 例
相 同 点	都有两种相关联的量，一种量变化，另一种量也随着变化。
不 同 点	商一定 　　y/x= k（一定）	积一定 　　x×y=k（一定）

人教版小升初数学知识要点整理.doc

本文来源：https://www.wddqw.com/R6TX.html