【#中考# 导语】如何快速解决好等腰三角形问题，做到孰能生巧？今天®文档大全网总结了以下四种和等腰三角形题型有关的常见辅助线添加方法，共5道例题，有详细讲解。

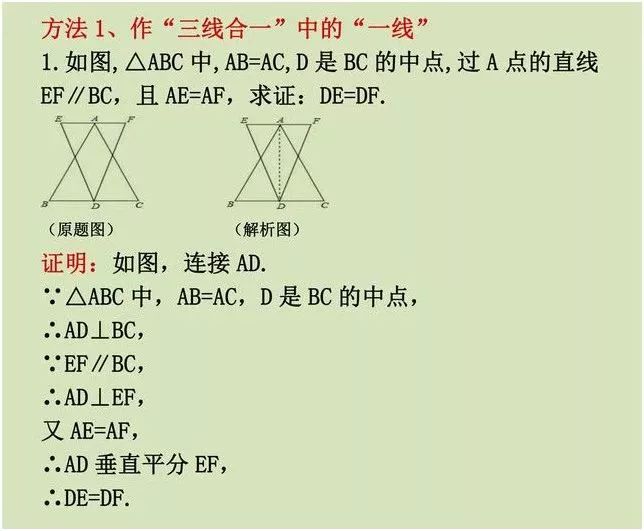
方法一：做三线合一中的一线

三线合一，是等腰三角形里最重要的性质定理之一。所谓三线，就是等腰三角形中，顶角的角平分线，底边的中线，底边的高线。必然三线合一。

例题1，是三线合一的最基础的题型，D是BC的中点，那么连接AD，通过三线合一的性质，得出AD⊥BC.

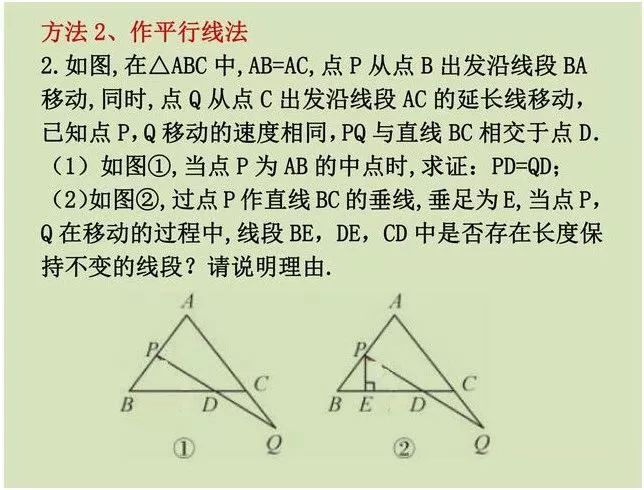
方法二：做平行线法

这个一般是做一腰的平行线，得出两个角相等，从而得出三角形全等

例题2中，这个题是非常常见的考试经典题型。第①小题，得出三角形全等，得出PD=QD。

第②小题，过点P做PF∥AC，因为△PBF是等腰三角形，PE⊥BF，三线合一得出BE=EF。又因为三角形全等，得出FD=CD。所以，得出ED=BC的一半，即为定值。

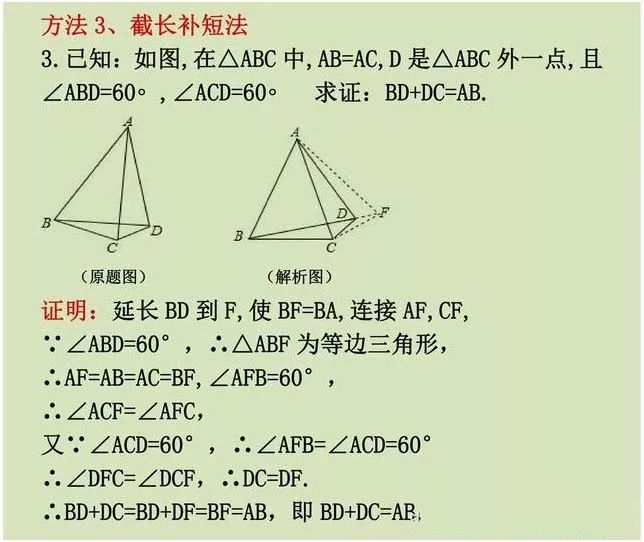
方法三：截长补短法，或者叫截长取短法

简单说，就是在某一条线段上截取一条线段，和已知线段相等。或者，延长某一线段，使之等于某已知线段。此解题方法常用，请大家细心钻研，平时多探索，勤学苦练。

例题3，就是一道延长某一线段，使之等于某已知线段，经典考试题型。

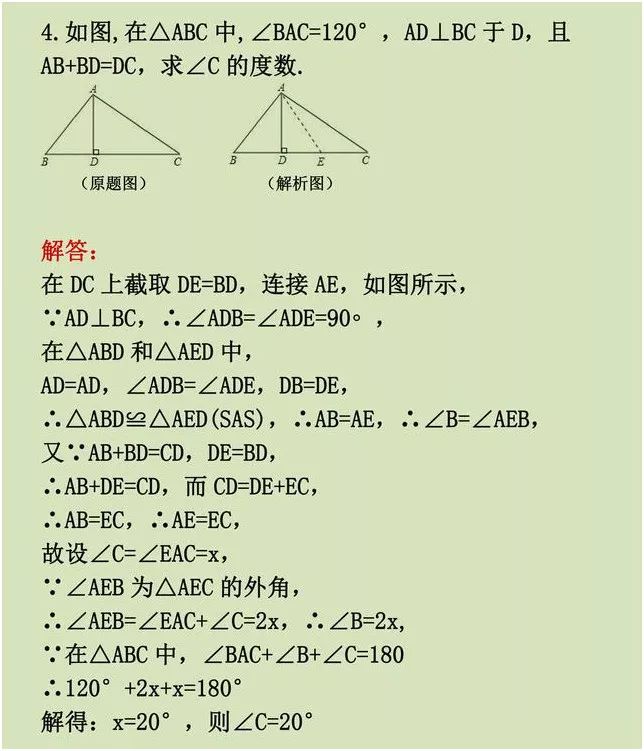
例题4，这就是一道在某一条线段上截取一条线段，和已知线段相等，通过等量转换，得出结论的经典考试题型。

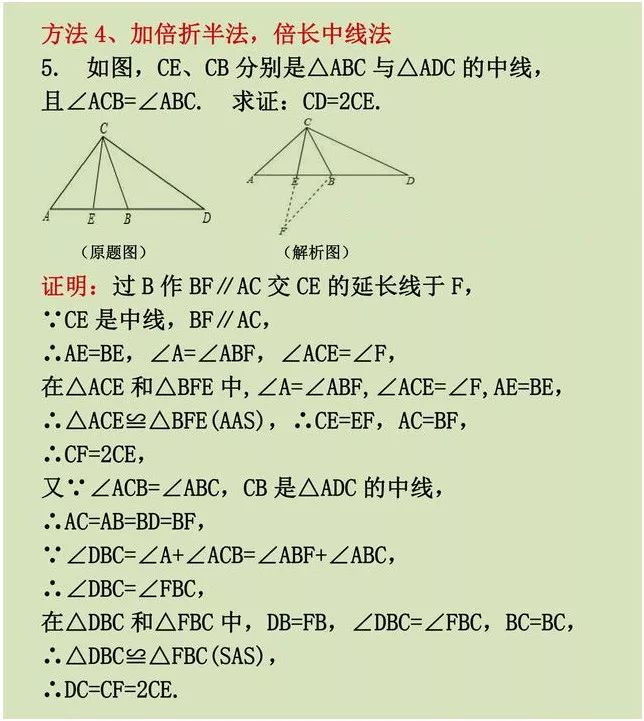
方法四：加倍折半法，倍长中线法

例题5，解析说过点B做BF∥AC，最后得出的还是线段相等。

其实，这个题还有一个更好的解题思路，就是倍长中线法

先提示一下辅助线的添加方法。因为CE是△ABC的中线，倍长中线CE。延长CE至F，使EF=CE，连接BF。倍长中线，必出三角形全等，最后得出，△DBC≌△FBC，所以DC=CF，所以CD=2CE。

看完这经典例题之后，不要认为自己就完全掌握了，这个时候要干什么？

当然是在自己的练习题中找几道相似的题，加以运用强化一下！

本文来源：https://www.wddqw.com/hbtu.html