2018上海中考数学:2018中考数学知识点【五篇】
【#中考# 导语】海阔凭你跃,天高任你飞。愿你信心满满,尽展聪明才智;妙笔生花,谱下锦绣文章;冷静细心,发挥如鱼得水;心想事成,努力备考,考到理想院校!以下是®文档大全网为大家整理的 《2018中考数学知识点【五篇】》供您查阅。
【第一篇:一次函数】
一次函数的定义
一次函数,也作线性函数,在x,y坐标轴中可以用一条直线表示,当一次函数中的一个变量的值确定时,可以用一元一次方程确定另一个变量的值。
函数的表示方法
列表法:一目了然,使用起来方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律。
解析式法:简单明了,能够准确地反映整个变化过程中自变量与函数之间的相依关系,但有些实际问题中的函数关系,不能用解析式表示。
图象法:形象直观,但只能近似地表达两个变量之间的函数关系。
一次函数的性质
一般地,形如y=kx+b(k,b是常数,且k≠0),那么y叫做x的一次函数,当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数
注:一次函数一般形式y=kx+b(k不为0)
a).k不为0
b).x的指数是1
c).b取任意实数
一次函数y=kx+b的图像是经过(0,b)和(-b/k,0)两点的一条直线,我们称它为直线y=kx+b,它可以看做直线y=kx平移|b|个单位长度得到。(当b>0时,向上平移;b<0时,向下平移)具体如下:
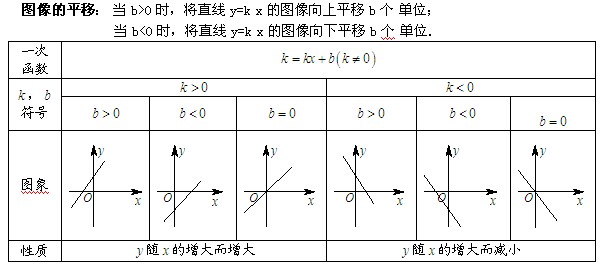
【第二篇:有关圆的字母表示方法】
有关圆的字母表示方法
圆--⊙半径—r弧--⌒直径—d
扇形弧长/圆锥母线—l周长—C面积—S三、有关圆的基本性质与定理(27个)
1.点P与圆O的位置关系(设P是一点,则PO是点到圆心的距离):
P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO
2.圆是轴对称图形,其对称轴是任意一条过圆心的直线。圆也是中心对称图形,其对称中心是圆心。
3.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
4.在同圆或等圆中,如果2个圆心角,2个圆周角,2条弧,2条弦中有一组量相等,那么他们所对应的其余各组量都分别相等。
5.一条弧所对的圆周角等于它所对的圆心角的一半。
6.直径所对的圆周角是直角。90度的圆周角所对的弦是直径。
7.不在同一直线上的3个点确定一个圆。
8.一个三角形有确定的外接圆和内切圆。外接圆圆心是三角形各边垂直平分线的交点,到三角形3个顶点距离相等;内切圆的圆心是三角形各内角平分线的交点,到三角形3边距离相等。
9.直线AB与圆O的位置关系(设OP⊥AB于P,则PO是AB到圆心的距离):
AB与⊙O相离,PO>r;AB与⊙O相切,PO=r;AB与⊙O相交,PO
10.圆的切线垂直于过切点的直径;经过直径的一端,并且垂直于这条直径的直线,是这个圆的切线。
11.圆与圆的位置关系(设两圆的半径分别为R和r,且R≥r,圆心距为P):
外离P>R+r;外切P=R+r;相交R-r
【第三篇:圆的相关量的定义】
圆及圆的相关量的定义
1.平面上到定点的距离等于定长的所有点组成的图形叫做圆。定点称为圆心,定长称为半径。
2.圆上任意两点间的部分叫做圆弧,简称弧。大于半圆的弧称为优弧,小于半圆的弧称为劣弧。连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。
3.顶点在圆心上的角叫做圆心角。顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。
4.过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心。和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为内心。
5.直线与圆有3种位置关系:无公共点为相离;有2个公共点为相交;圆与直线有公共点为相切,这条直线叫做圆的切线,这个的公共点叫做切点。
6.两圆之间有5种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有公共点的,一圆在另一圆之外叫外切,在之内叫内切;有2个公共点的叫相交。两圆圆心之间的距离叫做圆心距。
7.在圆上,由2条半径和一段弧围成的图形叫做扇形。圆锥侧面展开图是一个扇形。这个扇形的半径成为圆锥的母线
【第四篇:函数定义域】
确定函数定义域的方法
(1)关系式为整式时,函数定义域为全体实数;
(2)关系式含有分式时,分式的分母不等于零;
(3)关系式含有二次根式时,被开放方数大于等于零;
(4)关系式中含有指数为零的式子时,底数不等于零;
(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
用待定系数法确定函数解析式的一般步骤
(1)根据已知条件写出含有待定系数的函数关系式;
(2)将x、y的几对值或图像上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程
(3)解方程得出未知系数的值;
(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式。
【第五篇:正比例函数和一次函数】
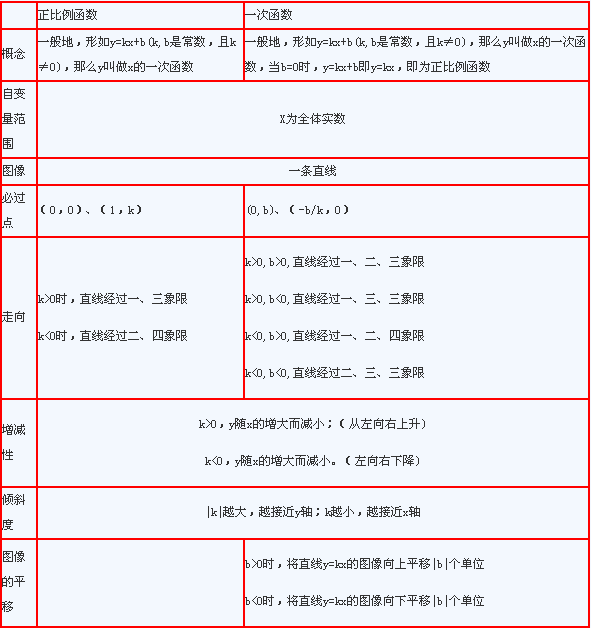
正在阅读:
2018中考数学知识点【五篇】03-11
七年级奥数加减消元法知识点大全201701-01
我的老师作文550字09-04
2021年江西九江中级审计师报名时间:6月7日-16日07-18
考前誓师动员大会主持稿12-04
党员个人自查报告【七篇】08-20
2017年高考作文范文1000字:一把难以让我释怀的雨伞11-15
2016年计算机等级考试一级Photoshop操作辅导:球中字04-08
试用期主要工作报告01-29
冬日里的一抹阳光作文800字05-26